Par Tidiane CISSE & Yasmine BELHADRI

Introduction
Netflix est une compagnie qui gère une très large collection de show télévisé et de films en streaming accessibles à n’importe quel moment de la journée (Ordinateur, télévision). Cette entreprise est rentable car ses clients effectuent mensuellement un virement pour avoir accès aux services de la plateforme. Néanmoins, les clients Netflix ont aussi la possibilité de rompre leur contrat à n’importe quel moment.
Il est vital pour le business Netflix de faire en sorte que les utilisateurs soient dépendants de la plateforme afin de ne pas perdre sa clientèle.
C’est grâce à son système de recommandation que Netflix permet de rester leader du marché dans le domaine du streaming en alimentant quotidiennement le feed des utilisateurs par des suggestions de séries ou de films.
Le système de recommandation de Netflix prend en compte non seulement l’information concernant l’utilisateur mais aussi les différents items qu’ils consomment quotidiennement.
Il existe plusieurs algorithmes disponibles qui permettent de modéliser un système de recommandations.
Dans ce dossier on va essayer de mieux comprendre L’algorithme de recommandation de Netflix, en se focalisant sur différents outils utilisés sur la plateforme. Nous avons également soumis un questionnaire en ligne pour récupérer les avis concernant le système de recommandation de Netflix que nous présenterons en annexe.
A. Algorithmes de filtrage collaboratif
Les algorithmes de filtrage collaboratif reposent sur l’idée que si deux clients ont un historique de notation similaire, ils se comporteront de la même manière à l’avenir (Breese, Heckerman et Kadie, 1998). Si, par exemple, il y a deux utilisateurs très probables et que l’un d’entre eux regarde un film et lui attribue un bon score, cela indique que le second utilisateur aura un comportement similaire. Il s’agit d’une méthodologie utile car elle ne repose pas sur des informations supplémentaires sur les éléments (acteurs, réalisateur, genres, par exemple) ou sur l’utilisateur (informations démographiques, par exemple) pour produire des recommandations. Les suggestions générées par cette méthodologie peuvent être une recommandation spécifique ou une prédiction (Isinkaye, Folajimi et Ojokoh, 2015).
Dans cette partie, nous allons utiliser des notions mathématiques pour mieux expliquer cet algorithme :
- Supposons une collection d’utilisateurs ui, et une collection de produits dans notre cas, les films pj, où i = 1, . . . , n et j = 1,. . . , m. L’ensemble de données doit être organisé sous la forme d’une matrice V n x m d’éléments utilisateur, de notations vi, j, avec vi, j vide si l’utilisateur n’a pas noté le film pj. En d’autres termes, les utilisateurs sont représentés par les lignes et les films par les colonnes, les entrées de la matrice V sont les évaluations, sur une échelle d’un à cinq.

Étant donné que le filtrage collaboratif est basé sur des informations relatives à des utilisateurs similaires ou à des éléments similaires, les FC pourraient être classés en deux approches différentes : techniques basées sur la mémoire et techniques basées sur un modèle .
a) Technique basée sur la mémoire
Les approches de filtrage collaboratif basé sur la mémoire peuvent être divisées en deux sections principales : le filtrage collaboratif basé sur l’utilisateur et le filtrage collaboratif basé sur les items (Liang et al. (2016)). Où Les recherches par utilisateur trouvent des utilisateurs à l’interface similaires, en fonction de la similarité des évaluations, et recommandent des produits appréciés par ces utilisateurs. D’autre part, les filtres basés sur les éléments selon l’élément pj (matrice V ci-dessus ), recherchent les utilisateurs qui ont aimé cet élément, puis recherchent les différents éléments qui ont plu à ces utilisateurs, c’est ainsi que les recommandations sont effectuées à l’aide de ces éléments.
Le filtrage collaboratif basé sur l’utilisateur a pour objectif principale d’identifier les utilisateurs ayant des valeurs de notation similaires et leur proposer parmi les nouveaux éléments les mieux cotés en fonction de leurs préférences (Hahsler, 2014). Il existe une grande variété de paramètres permettant de comparer la similarité entre les vecteurs ou de rechercher le voisin le plus proche (dans notre cas, les utilisateurs). Les plus populaires sont la similarité des cosinus ou la corrélation de Pearson (Amatriain et al., 2011, Breese, Heckerman et Kadie, 1998). La similarité de cosinus calcule le cosinus de l’angle entre ces deux vecteurs utilisateurs.
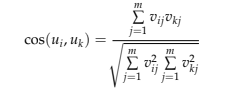
La corrélation de Pearson mesure la force d’une association linéaire entre deux vecteurs (Melville, Mooney et Nagarajan, 2002).
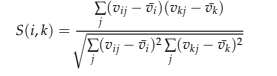
À partir de l’équation ci-dessus, S (i, k) calcule la similarité entre deux utilisateurs ui et uk, où vij est la note attribuée par l’utilisateur ui au film p, vi est la note moyenne attribuée par l’utilisateur ui.
Avec ce score de similarité, nous pouvons comparer chaque utilisateur parmi le reste des n-1 utilisateurs. Plus la similarité entre les vecteurs est élevée, plus la similarité entre les utilisateurs est grande. On obtient ainsi une matrice symétrique n × n avec le score de similarité de tous les utilisateurs, défini comme la matrice de similarité S.

Tout d’abord, il est nécessaire d’identifier le groupe d’utilisateurs le plus similaire à l’utilisateur actif (ui), c’est-à-dire en sélectionnant les k premiers utilisateurs (k-voisins les plus proches) ayant le score de similarité le plus élevé avec l’utilisateur ui. L’étape suivante consiste à identifier les produits que ces utilisateurs similaires ont aimés, à supprimer les films qu’il a déjà vus, à peser les films que les utilisateurs les plus similaires ont visionnés à l’aide des similarités sous forme de poids et à ajouter les valeurs. Le résultat final est une prédiction des taux que l’utilisateur donnerait à chacun de ces films. La dernière étape consiste à sélectionner les N premiers films en fonction du classement prévu. Ensuite, la prévision d’une recommandation est basée sur la combinaison pondérée de la notation du voisin sélectionné, c’est l’écart pondéré de la moyenne du voisin (Isinkaye, Folajimi et Ojokoh, 2015) ; décrite par l’équation ci-dessous :
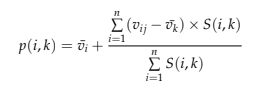
Nous allons maintenant aborder le filtrage collaboratif basé sur les items filtrage.
Rappelons dans la section ci-dessus, l’algorithme était basé sur les utilisateurs et les étapes d’identification des recommandations consistaient d’abord à identifier les utilisateurs similaires en termes d’achat des mêmes éléments, puis à recommander à un nouvel utilisateur les éléments que d’autres utilisateurs avaient acquis. Maintenant, l’approche est le contraire. L’algorithme commence à rechercher les utilisateurs similaires en fonction des achats et des préférences. En d’autres termes, il essaye de déterminer à quel point un film est similaire à un autre. L’idée maitresse est de calculer la similarité entre deux éléments pj et pl, en séparant les utilisateurs qui ont déjà regardé et évalué les deux films, puis d’utiliser l’une des techniques permettant de calculer la similarité entre les éléments, par exemple, la similarité basée sur le cosinus, ainsi que la similarité basée sur la corrélation ou la similarité cosinus ajustée (Sarwar et al., 2001).
Dans la similarité basée sur le cosinus, les deux éléments sont considérés comme deux vecteurs dans l’espace utilisateur n dimensionnel où la différence d’échelle d’évaluation entre les utilisateurs n’est pas prise en compte. Pour la similarité basée sur la corrélation, la corrélation de Pearson-r est calculée, mais il est important d’isoler les cas où les utilisateurs ont évalué j et l, où U représente les utilisateurs qui ont évalué les deux films (Sarwar et al. (2001)).
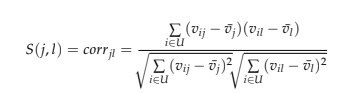
Ici, vij indique la cote de l’utilisateur ui en U sur le film pj, et v ̄j la cote moyenne du j-ème film. Si les évaluations des utilisateurs ont une échelle différente, nous pouvons utiliser la similarité de cosinus ajustée, où la moyenne évaluée par l’utilisateur est soustraite de chaque paire cotée (Sarwar et al., 2001).
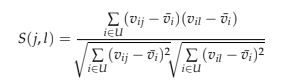
Ici, vi est la moyenne des cotes attribuées par le i -ème utilisateur en U. Analogue à la CF basée sur l’utilisateur, nous nous retrouvons avec une matrice de similarité, mais dans ce cas, la dimension est m × m, ce qui reflète la similarité de tous les films. Les uns aux autres, et à partir de ces scores, nous pouvons générer des recommandations pour les utilisateurs. Ensuite, les éléments que les utilisateurs ont précédemment évalués sont sélectionnés, les films qui leur ressemblent le plus sont sélectionnés et pesés, et enfin, nous obtenons une recommandation de films que l’utilisateur n’a pas encore vus.
b) Techniques basées sur des modèles
Les notations sont utilisées pour mettre en œuvre un modèle qui améliorera les résultats du filtrage collaboratif afin de trouver des modèles dans les données. Pour construire un modèle, certains algorithmes d’exploration de données ou d’apprentissage automatique peuvent être appliqués. Ces types de modèles sont très utiles pour recommander un ensemble de films de la manière la plus rapide et afficher des résultats similaires aux modèles basés sur la mémoire. Les techniques basées sur des modèles sont basées sur la factorisation matricielle (MF), qui est très populaire car il s’agit d’une méthode d’apprentissage non supervisée pour la réduction de la dimensionnalité. Fondamentalement, MF apprend les préférences latentes des utilisateurs et des éléments des évaluations afin de prédire les évaluations manquantes, en utilisant le produit scalaire des caractéristiques latentes des utilisateurs et des éléments (Girase et Mukhopadhyay, 2015). Certaines des techniques pouvant être appliquées sont basées sur les techniques de réduction de la dimensionnalité, telles que l’analyse en composantes principales (ACP), la décomposition en valeurs singulières (SVD), la factorisation matricielle probabiliste (PMF), la technique de complétion matricielle, les méthodes de sémantique latente et les méthodes de régression et de régression). Regroupement (Isinkaye, Folajimi et Ojokoh, 2015). Ci-dessous, nous avons décrit 3 des techniques les plus courantes: Analyse en composantes principales (ACP) Il s’agit d’une technique puissante permettant de réduire les dimensions de l’ensemble de données. Cette technique est considérée comme une réalisation de la MF (Ricci, Rokach et Shapira, 2011). L’analyse en composantes principales est connue en utilisant une transformation orthogonale, car elle utilise les vecteurs propres de la matrice de covariance. L’idée est de transformer un ensemble de variables pouvant être corrélées en un ensemble de nouveaux vecteurs non corrélés. Ces nouveaux vecteurs sont nommés composantes principales. Étant donné que l’objectif principal est de réduire les dimensions, l’ensemble des variables d’origine est supérieur au nombre final de composantes principales. Pour mieux comprendre cet algorithme, nous avons essayé d’analyser l’algorithme de popularité.
B. Algorithme de popularité
L’algorithme popularité se base sur la popularité des séries, c’est-à-dire les recommandations seront équivalentes aux films ou séries populaires (Si on considère que la collection des utilisateurs uj et une collections de services, dans notre cas des films pi , ou i = 1, . . . , n et j = 1, . . . , m. le data set doit être organisé n × m client- film matrice V, de ratings vi,j , avec vi,j NULL si l´utilisateur ui n’à pas noté le film pj . En gros l’utilisateur sera représenté par des index de lignes et les films par des colonnes. Les entrés de la matrice V seront nos ratings (de 1 á 5), ou le collaborative filtering qui se base sur les patterns de l´activité des utilisateurs pour produire par la suite une recommandation spéciale consommateur
Le content based filtering 1 et 2, ici la recommandation se fait en se basant sur les différents items qui contiennent la même information (fragmenter les vecteurs de donnes et les regrouper en cluster selon un indicateur de similarité inter/intra variance pour calculer le taux d’homogénéité des vecteurs de données), cette information est une combinaison de données qu´un utilisateur a aimé ou utilisé dans le passé.
Le réseau de neurones final permettra ainsi d’extraire des règles et des tendances à partir des données et comprendre mieux le phénomène lié au système de recommandation de Netflix.
En gros, l’idée est de recommander les films les plus populaires aux utilisateurs. Ils pourraient être les plus regardés, ou aussi ceux avec les meilleures notes. Les recommandations de popularité peuvent être créées en fonction des données d’utilisation et du contenu de l’article. De manière surprenante, une telle approche a généralement un effet puissant sur le comportement de l’utilisateur (Bressan et al, 2016). Par exemple, dans les portails de nouveautés où il y a des sections comme « Nouveautés populaires » et ensuite subdivisé en sections. Cette approche est relativement facile à mettre en œuvre, par exemple, il existe plusieurs bons algorithmes de base. Cela est particulièrement utile lorsque l’utilisateur est nouveau dans le système et qu’il n’a visionné ou évalué aucun film, en d’autres termes, lorsque nous ne comptons pas sur des informations concernant le client. Cependant, en recommandant les items les plus populaires, nous n’avons que peu d’occasions d’apprendre, c’est-à-dire que le système ne recommandera pas de nouveaux articles et n’apprendra pas des suggestions du passé. De plus, la liste de recommandations peut rester la même. Certaines méthodes plus élaborées sont le filtrage collaboratif ou le filtrage basé sur le contenu
C. Peut-on dire que l’algorithme de Netflix est fantastique ?
Selon le site belge cinergie, cet algorithme est d’une puissance extraordinaire analyse les habitudes de ses clients : quel type de films regardez-vous le plus ? Quand arrêtez-vous la lecture ? À quel volume le regardez-vous et quand le changez-vous ? etc. Avec toutes ces données, Netflix vous recommande des programmes qui ne seront pas les mêmes le mardi à 15h ou le mercredi à 22h. Ce système est plébiscité par les clients puisque plus de 8 visionnages sur 10 sont issus des recommandations de l’algorithme. Ceux qui effectuent des recherches peuvent aussi compter sur un choix de genres impressionnant, 76 000 environ – pour 100 000 titres. Des genres aussi précis que farfelus tels que » Comédies romantiques des années 80 se déroulant à Moscou » ou » Films de requins mutants affrontant des monstres ». Un algorithme qui s’affine toujours davantage, 300 millions d’heures de visionnages seraient ainsi analysés chaque semaine. 900 ingénieurs sur les 2000 employés que compte l’entreprise sont dédiés à cette tâche. Netflix l’intègre également dans son système de production.
Encore selon ce site, le système de recommandation de Netflix est appelé prédictif et est censé devancer les envies. Rappelons que ce sont les actions passées qui se trouvent récupérées, stockées et recoupées. Les désirs ne sont pas devancés, ils sont encadrés, savamment et sagement guidés. On assisterait en cas de généralisation définitive de ce système à une évolution majeure de nos sociétés actuelles.
On est dans un schéma ou l’offre devance la demande. On peut supposer que l’entreprise modifie ses recommandations arbitrairement dans un but financier ou idéologique, comment le savoir ? se posent les questions de l’uniformisation de la création et de la pensée voire, à terme, le contrôle de la pensée. Il faut rappeler que les entreprises ne dévoilent pas leurs algorithmes, protégés par le secret industriel.
Au regard de toutes les informations que nous avons obtenues, nous pouvons donc affirmer que cet algorithme est puissant et fantastique.
Conclusion
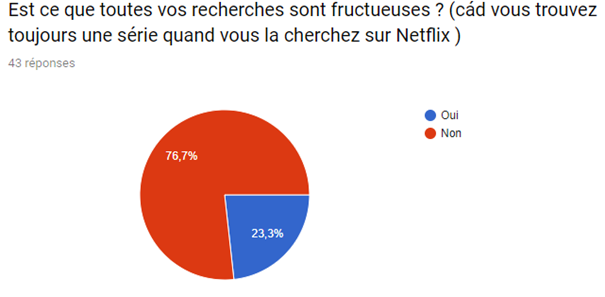
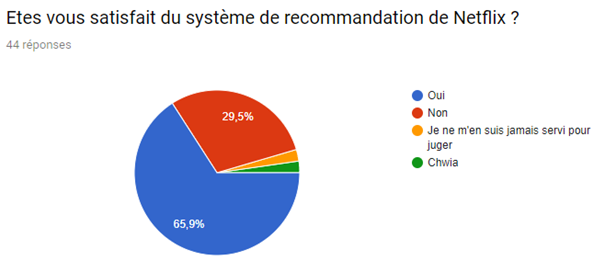
Bien que la plateforme ne contienne pas la totalité des séries et des films, les utilisateurs restent malgré tout satisfait de ses services comme la démontrer notre enquête ci-dessous.
Si le système de recommandation de Netflix et une compilation d’algorithme ce
dernier reste l’un
des plus efficace voir le plus performant.
Nous avons pour but d´ ici la fin de notre formation pouvoir créer une plateforme en utilisant le concept de datawarehouse et y implémenter ces algorithmes afin de de modéliser ce système de recommandation á partir des ratings.
Webographies
Annexe :
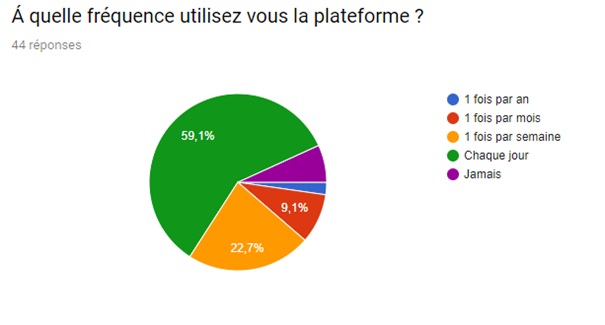
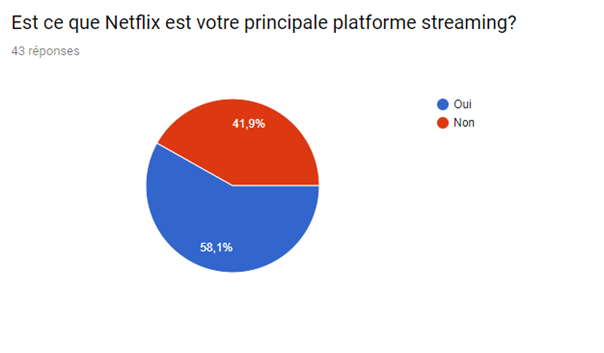
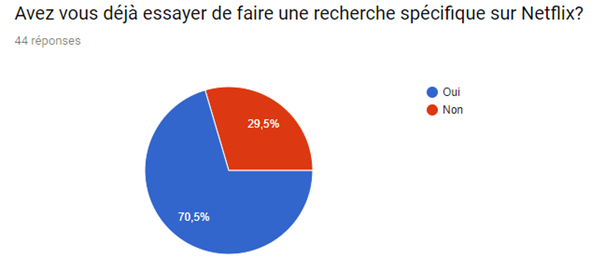
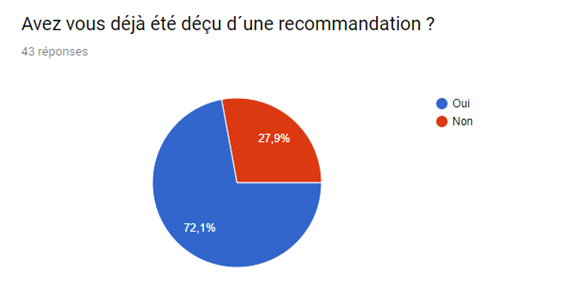
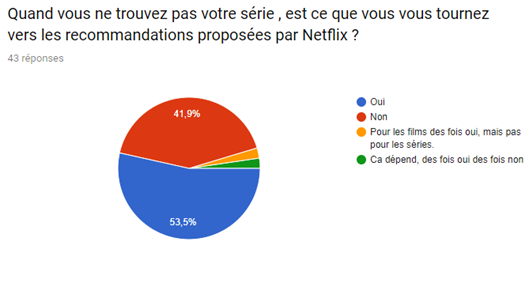
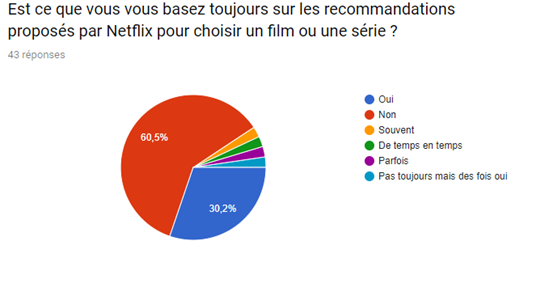
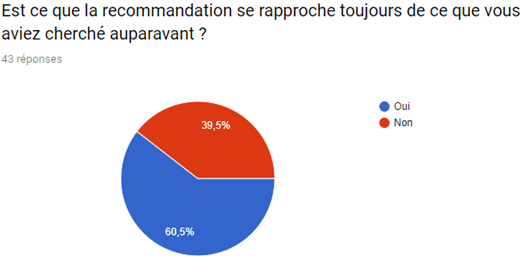
Nous avons réalisé un sondage afin de mieux visualiser le pouvoir du système de recommandation sur le consommateur et de la satisfaction de ce dernier malgré le fait que de nombreux films et séries sont indisponibles.